所謂「實驗」就是一系列的試驗，在執行這些試驗時，我們故意變動系統中輸入變數的設定值，藉此觀察輸出反應值變動的理由與趨勢，這就是「實驗」。而實驗設計DOE (Design of Experiment) 就是運用統計手法，有系統的規劃實驗的條件組合，更有效率地獲取合理的實驗資料、提高分析結果的可靠性。
舉例來說，我們有興趣知道哪一種原物料，可使生產出來的產品硬度最高，在此實驗中，輸入變數即為「原物料」，輸出反應值即為「產品硬度」，這些我們關心的輸出反應值被稱為「反應變數」(Response)，而可能影響反應變數的輸入變數則稱為「因數」(Factor)，而因數的設定值則稱為「水準」(Level) 。
實驗設計的目的在於設計良好的試驗條件，使從可能影響反應變數的因數中，找出真正有影響的因數，並進一步尋找該因數在哪種水準值時能讓反應變數更接近期望。 不論是為了縮短新產品研發時程，或改善製程以提升更好的產品品質，「實驗」都扮演著極重要的角色。 透過實驗設計法可規劃出快速且有效率的實驗方法，找出影響產品特性之重要參數，以達到成本控制、降低製程變異及提升製程良率等功效。

全因數設計法

Full Factorial Design。包含所有的因數組合，此種實驗設計法所獲取的信息量是最充分的，能準確的估計所有實驗因數的主效應，能估計的因數交互作用也是最多的，但缺點是實驗次數過多，使成本倍增。

二因數部分因數設計法

Regular 2-level Fractional Factorial Design。所有因數皆為二水準，且可透過 1/2減半實驗、1/4實驗、1/8實驗等大幅減少實驗次數，因此很適合用於實驗初期的篩選實驗 (screening experiments)，目的是從大量的因數中篩選出顯著因數，以縮小實驗範圍去進入下一實驗階段，但缺點是並非所有交互作用項皆可估計。

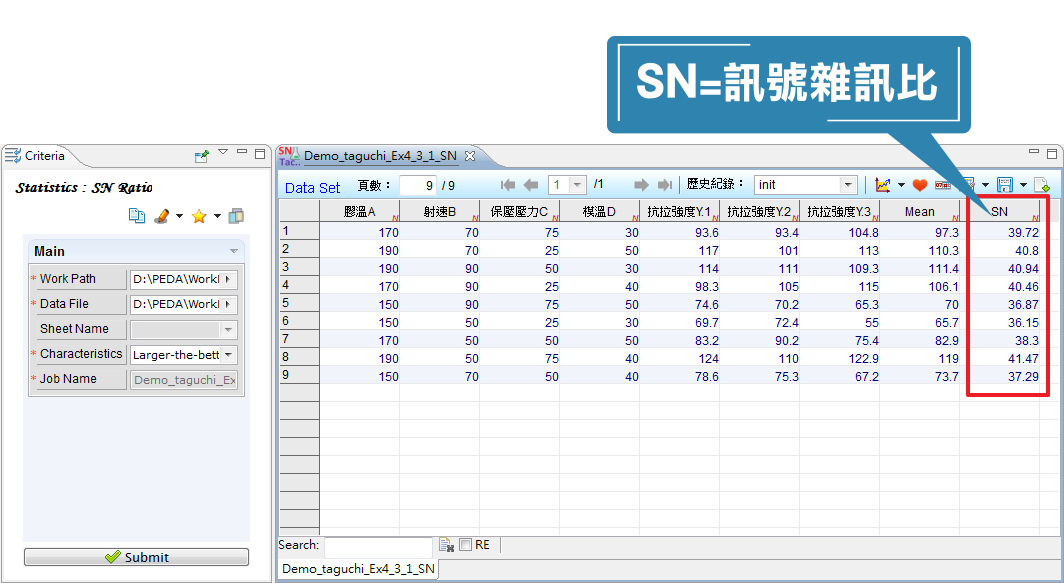
田口方法（Taguchi Method）的穩健參數設計，為一廣泛被工業界應用的實驗設計法，特點在於降低實驗次數與成本，同時考慮製程上其他難以控制的因素（譬如環境因素）對品質特性的影響，找出能使產品品質穩定、對生產過程中的雜訊不敏感的方法。

BBD（Box-Behnken Design）

反應曲面法之 Box-Behnken 設計。若因數與反應變數之間存在著二次關係式時，因數設計法已不足以使用，需改用反應曲面法；BBD 也是反應曲面法中很廣為人知的一種方法，優點是實驗次數較少。

CCD（Central Composite Design）

反應曲面法之中央合成設計。若因數與反應變數之間存在著二次關係式時，因數設計法已不足以使用，需改用反應曲面法；CCD 是一個配適二階模型非常有效率的設計。

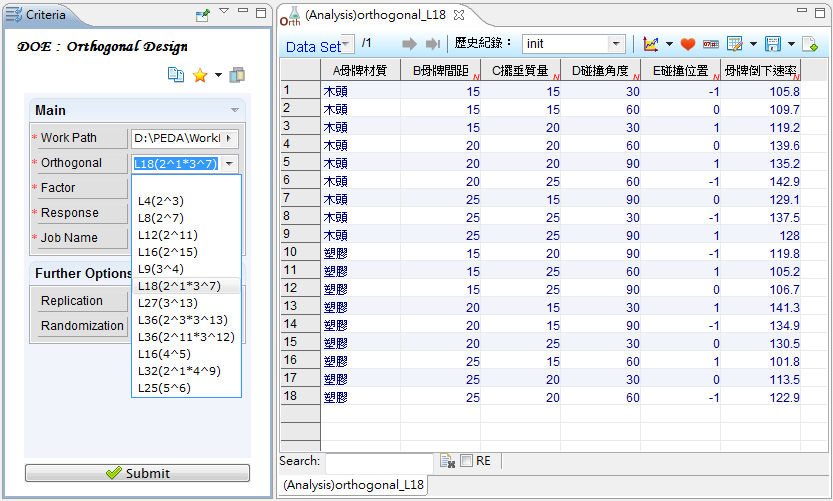
直交表設計法

Orthogonal Design。直交表提供了有系統且有效率地變動因數的方法，使得能以較少的實驗次數來獲得有用的統計資訊，是兼顧實驗成本及精確度的折衷方法；但由於並非所有水準組合都執行，故最佳設計組合可能不在直交表實驗組中，且並非所有交互作用項皆可估計。

D型最適化設計

D-Optimal Design。此設計法旨在最小化迴歸係數向量聯合信賴區域的體積，使迴歸係數之可靠度為最大；特點是可自行選擇實驗次數，並可設定因數間的限制關係，如研磨時"研磨時間-因數A"與"研磨力道-因數B"不能超過某一定值，否則被研磨物會破裂。

我們提供完善的統計分析手法，在您做完實驗、回報實驗數據後，直接執行該實驗設計法所擁有之所有統計分析，協助您尋找最佳因數設定值。

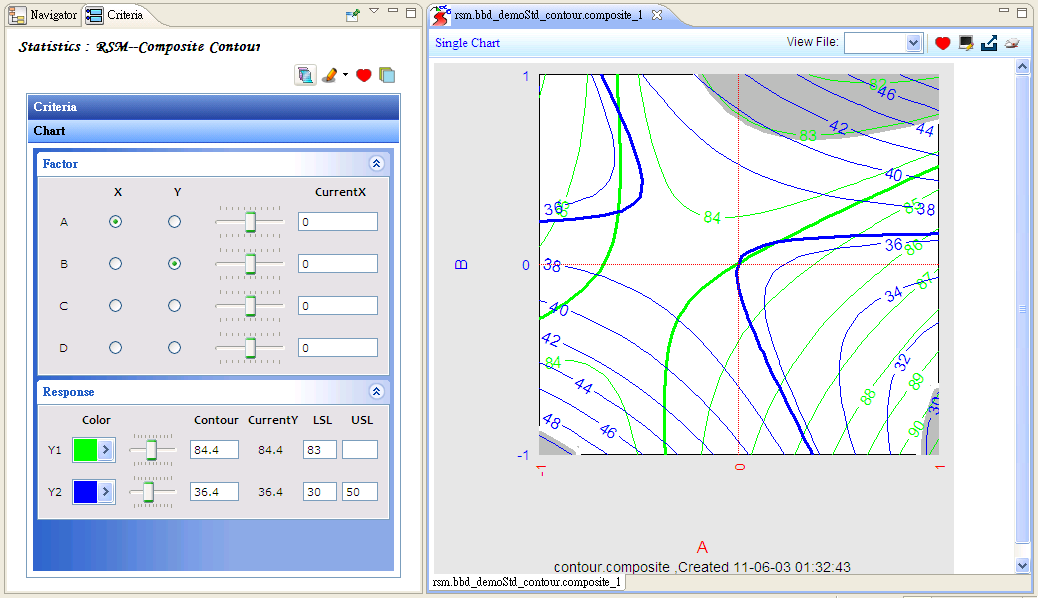
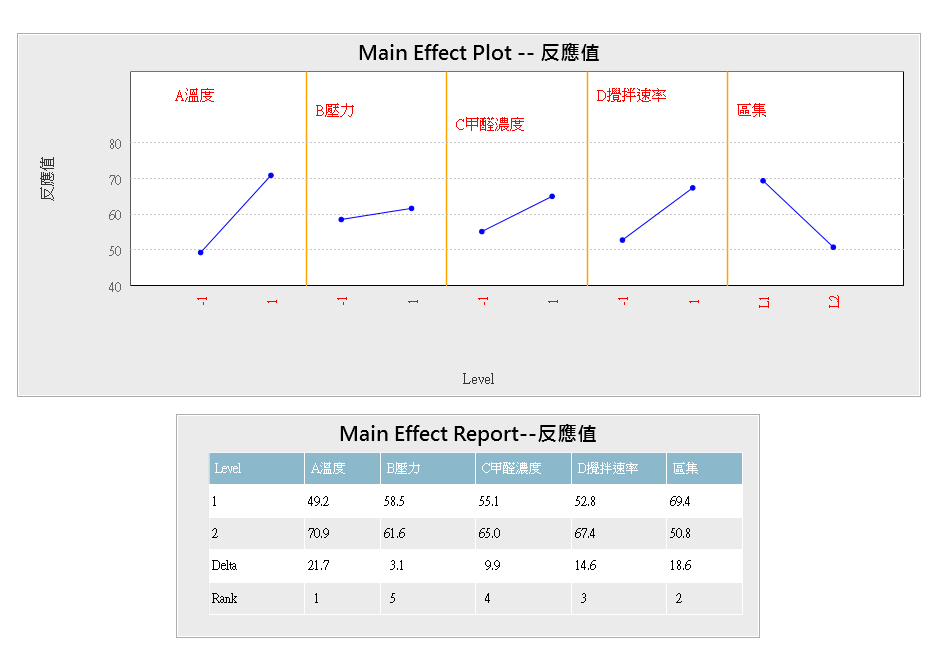
「效應分析」可解析某因數在水準值的改變下，對反應變數的影響，並可透過交互作用圖觀察因數間是否存在交互作用；或是利用「變異數分析」，將實驗中的總變異量拆解成多個欲探討的變異來源，藉此檢視實驗因數是否重要；透過「迴歸分析」可描述因數與反應變數之間的關係，將其建立成模型，透過模型的建置可進行預測、製程最佳化等；反應曲面法之「複合式等高線圖」，將多個反應變數之等高線圖重複堆疊，藉由圖形化的呈現讓使用者更清楚觀察反應變數的變化趨勢，但由於等高線圖是 2D 的，僅能同時觀察兩個因數與反應變數的關係，此時其他因數需被固定於定值；反應曲面法之「反應變數預測函數」提供一種方法可同時衡量多個反應變數，它將多個反應變數透過願望函數(Desirability Function)轉換成一個值，透過最大化此數值來尋找實驗的最佳因數設定值。