所谓「实验」就是一系列的试验，在执行这些试验时，我们故意变动系统中输入变量的设定值，藉此观察输出反应值变动的理由与趋势，这就是「实验」。而实验设计DOE (Design of Experiment) 就是运用统计手法，有系统的规划实验的条件组合，更有效率地获取合理的实验资料、提高分析结果的可靠性。
举例来说，我们有兴趣知道哪一种原物料，可使生产出来的产品硬度最高，在此实验中，输入变量即为「原物料」，输出反应值即为「产品硬度」，这些我们关心的输出反应值被称为「反应变量」(Response)，而可能影响反应变量的输入变量则称为「因子」(Factor)，而因子的设定值则称为「水平」(Level) 。
实验设计的目的在于设计良好的试验条件，使从可能影响反应变量的因子中，找出真正有影响的因子，并进一步寻找该因子在哪种水平值时能让反应变量更接近期望。 不论是为了缩短新产品研发时程，或改善制程以提升更好的产品质量，「实验」都扮演着极重要的角色。 透过实验设计法可规划出快速且有效率的实验方法，找出影响产品特性之重要参数，以达到成本控制、降低制程变异及提升制程良率等功效。

全因子设计法

Full Factorial Design。包含所有的因子组合，此种实验设计法所获取的信息量是最充分的，能准确的估计所有实验因子的主效应，能估计的因子交互作用也是最多的，但缺点是实验次数过多，使成本倍增。

二因子部分因子设计法

Regular 2-level Fractional Factorial Design。所有因子皆为二水平，且可透过 1/2减半实验、1/4实验、1/8实验等大幅减少实验次数，因此很适合用于实验初期的筛选实验 (screening experiments)，目的是从大量的因子中筛选出显着因子，以缩小实验范围去进入下一实验阶段，但缺点是并非所有交互作用项皆可估计。

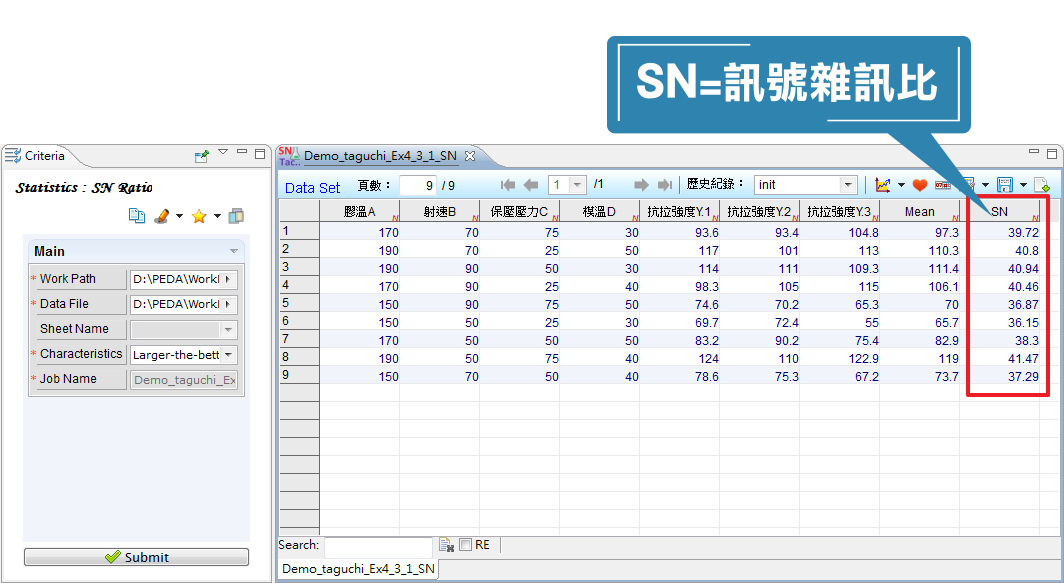
田口方法（Taguchi Method）的稳健参数设计，为一广泛被工业界应用的实验设计法，特点在于降低实验次数与成本，同时考虑制程上其他难以控制的因素（譬如环境因素）对质量特性的影响，找出能使产品质量稳定、对生产过程中的噪声不敏感的方法。

BBD（Box-Behnken Design）

反应曲面法之 Box-Behnken 设计。若因子与反应变量之间存在着二次关系式时，因子设计法已不足以使用，需改用反应曲面法；BBD 也是反应曲面法中很广为人知的一种方法，优点是实验次数较少。

CCD（Central Composite Design）

反应曲面法之中央合成设计。若因子与反应变量之间存在着二次关系式时，因子设计法已不足以使用，需改用反应曲面法；CCD 是一个配适二阶模型非常有效率的设计。

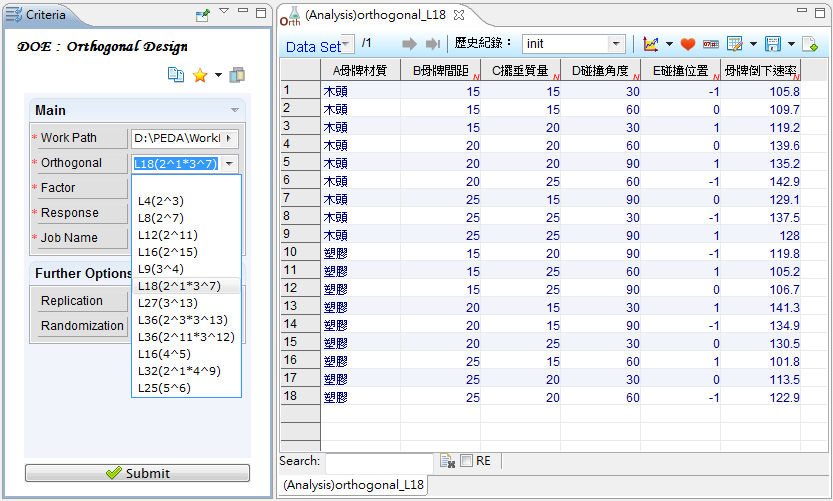
直交表设计法

Orthogonal Design。直交表提供了有系统且有效率地变动因子的方法，使得能以较少的实验次数来获得有用的统计信息，是兼顾实验成本及精确度的折衷方法；但由于并非所有水平组合都执行，故最佳设计组合可能不在直交表实验组中，且并非所有交互作用项皆可估计。

D型最适化设计

D-Optimal Design。此设计法旨在最小化回归系数向量联合信赖区域的体积，使回归系数之可靠度为最大；特点是可自行选择实验次数，并可设定因子间的限制关系，如研磨时"研磨时间-因子A"与"研磨力道-因子B"不能超过某一定值，否则被研磨物会破裂。

我们提供完善的统计分析手法，在您做完实验、回报实验数据后，直接执行该实验设计法所拥有之所有统计分析，协助您寻找最佳因子设定值。

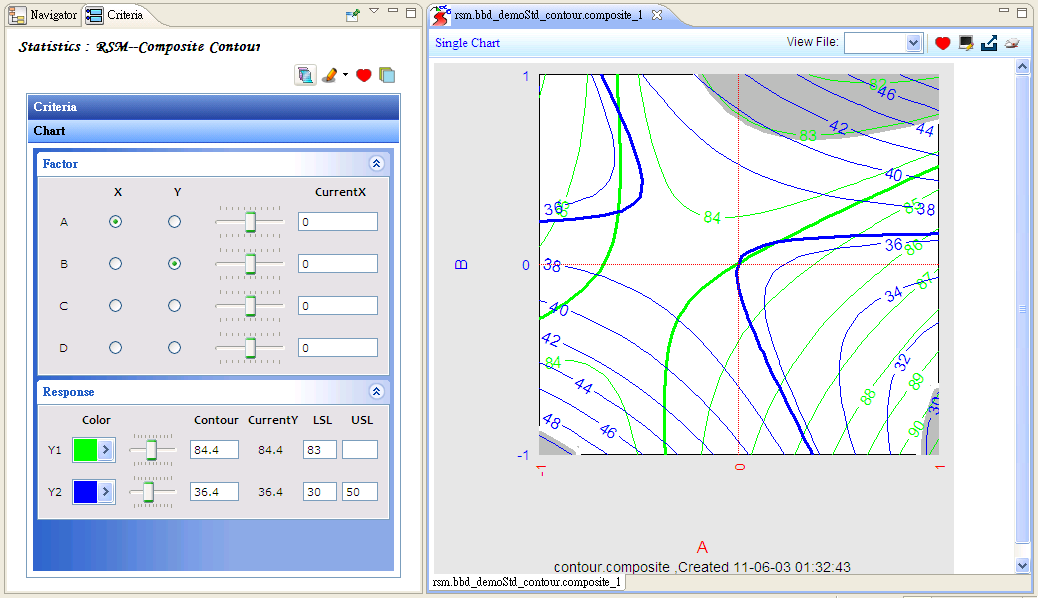
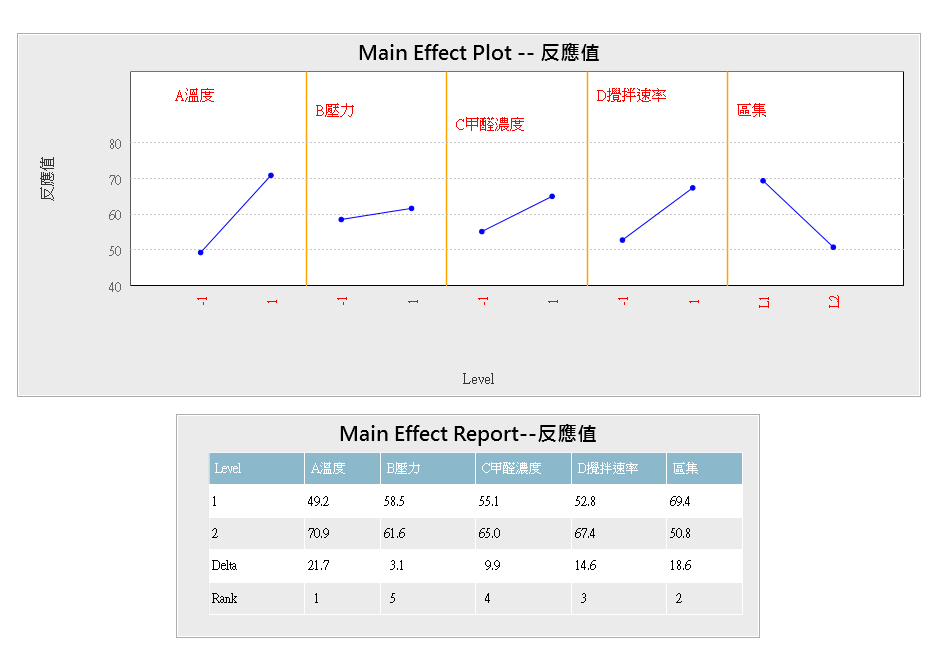
「效应分析」可解析某因子在水平值的改变下，对反应变量的影响，并可透过交互作用图观察因子间是否存在交互作用；或是利用「变异数分析」，将实验中的总变异量拆解成多个欲探讨的变异来源，藉此检视实验因子是否重要；透过「回归分析」可描述因子与反应变量之间的关系，将其建立成模型，透过模型的建置可进行预测、制程优化等；反应曲面法之「复合式等高线图」，将多个反应变量之等高线图重复堆栈，藉由图形化的呈现让用户更清楚观察反应变量的变化趋势，但由于等高线图是 2D 的，仅能同时观察两个因子与反应变量的关系，此时其他因子需被固定于定值；反应曲面法之「反应变量预测函数」提供一种方法可同时衡量多个反应变量，它将多个反应变量透过愿望函数(Desirability Function)转换成一个值，透过最大化此数值来寻找实验的最佳因子设定值。